반응형
지금까지(#1, #2, #3)와는 다른 방식으로 문제를 풀어본다.
그 동안은 대략 다음과 같은 과정으로 문제를 풀었다.
- 거리(D)를 구한다
- 거리(D)를 기반으로 최대 Flag개수(K)를 구한다
- 최대 Flag개수(K)를 검증한다
이번에는 배열A의 각 요소에서 가장 가까운 Peak값을 기록해두고, 이를 이용해서 전체 탐색을 줄여본다.
예시)
| A[0] | A[1] | A[2] | A[3] | A[4] | A[5] | A[6] | A[7] | A[8] | A[9] | A[10] | A[11] |
| 1 | 5 | 3 | 4 | 3 | 4 | 1 | 2 | 3 | 4 | 6 | 2 |
가장 가까운 Peak(next_peak) 정보를 추가해보자.
| A[0] | A[1] | A[2] | A[3] | A[4] | A[5] | A[6] | A[7] | A[8] | A[9] | A[10] | A[11] |
| 1 | 5 | 3 | 4 | 3 | 4 | 1 | 2 | 3 | 4 | 6 | 2 |
| 1 | 1 | 3 | 3 | 5 | 5 | 10 | 10 | 10 | 10 | 10 | -1 |
A[0]의 가장 가까운 Peak는 A[1]이다.
A[1]의 가장 가까운 Peak는 A[1]이다.
A[2]의 가장 가까운 Peak는 A[3]이다.
A[3]의 가장 가까운 Peak는 A[3]이다.
A[4]의 가장 가까운 Peak는 A[5]이다.
A[5]의 가장 가까운 Peak는 A[5]이다.
A[6]의 가장 가까운 Peak는 A[10]이다.
A[7]의 가장 가까운 Peak는 A[10]이다.
A[8]의 가장 가까운 Peak는 A[10]이다.
A[9]의 가장 가까운 Peak는 A[10]이다.
A[10]의 가장 가까운 Peak는 A[10]이다.
A[11]의 가장 가까운 Peak는 없다. (-1)
위 정보를 이용해서 탐색 횟수를 줄여보자.
총 Peak 개수(K): 4
K = 4, 탐색 1회차
| 현재위치 | 현재 위치의 next_peak | 설명(행동) |
| 0 | next_peak[0] = 1 | - next_peak[0] = 1에 flag를 세운다 (flag = 1) - 현재 위치를 next_peak[0] + K로 업데이트 한다 (현재위치 A[5]로 수정) |
K = 4, 탐색 2회차
| 현재위치 | 현재 위치의 next_peak | 설명(행동) |
| 5 | next_peak[5] = 5 | - next_peak[5] = 5에 flag를 세운다 (flag = 2) - 현재 위치를 next_peak[5] + K로 업데이트 한다 (현재위치 A[9]로 수정) |
K = 4, 탐색 3회차
| 현재위치 | 현재 위치의 next_peak | 설명(행동) |
| 9 | next_peak[9] = 10 | - next_peak[9] = 10에 flag를 세운다 (flag = 3) - 현재 위치를 next_peak[9] + K로 업데이트 한다 (현재위치 A[14]로 수정) |
A[14]는 존재하지 않으므로, 반복문 종료
위와 같은 방식으로 탐색을 하면, 시간복잡도는 \( O(N/K) \) 가 된다.
K값이 1에 가까운 값일수록 탐색 횟수가 N에 비례하여 증가하므로, 결국 전체 시간복잡도는 \( O(N) \) 이 된다.
코드 (C++)
int solution(vector<int> &A) {
//peak 구하기
vector<int> peaks = {};
for(size_t i = 1; i < A.size() - 1; i++)
{
if(A[i - 1] < A[i] && A[i] > A[i + 1])
{
peaks.emplace_back(i);
}
}
//예외처리
if(peaks.size() == 0) return 0;
else if(peaks.size() == 1) return 1;
//next_peak 구하기
vector<int> next_peak(A.size(), -1);
auto peak = peaks.begin();
for(int i = 0; i < static_cast<int>(next_peak.size()); i++)
{
if(i <= *peak)
{
next_peak[i] = *peak;
}
else // i > *peak
{
peak++;
if(peak == peaks.end()) break;
next_peak[i] = *peak;
}
}
//flag 개수 세기
int K = static_cast<int>(peaks.size());
while(K > 0)
{
int flag_cnt = 0;
size_t pos = 0; //현재 위치
while(pos < next_peak.size() && next_peak[pos] != -1)
{
//next_peak가 있으면, next_peak에 flag를 꽂는다
if(next_peak[pos] != -1) flag_cnt++;
//현재 위치 변경, flag를 꽂은 peak에서 +K만큼이동 시킨다
pos = next_peak[pos] + K;
}
if(flag_cnt >= K) return K;
K--;
}
return K;
}
결과
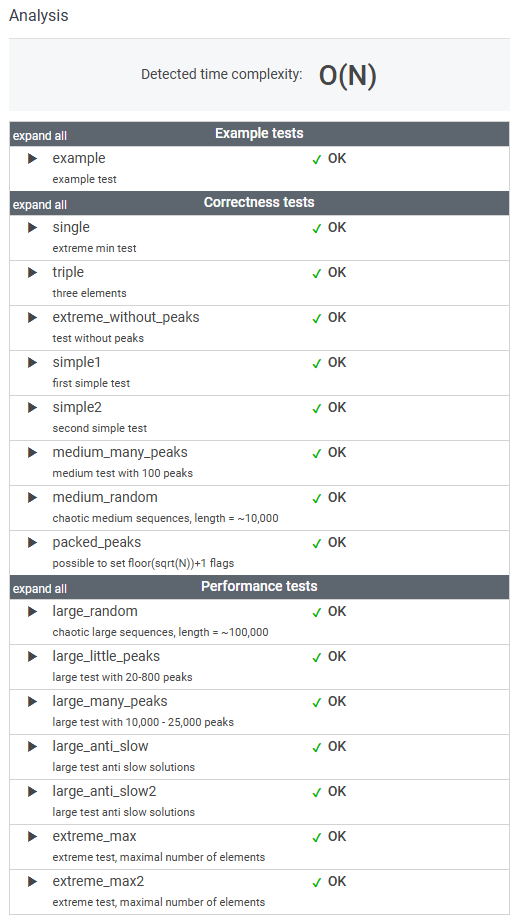
반응형
'Algorithm Problem > Codility' 카테고리의 다른 글
| Lesson 10. Prime and composite numbers - Peaks #2 (속도 개선-1) (0) | 2024.12.28 |
|---|---|
| Lesson 10. Prime and composite numbers - Peaks #1 (0) | 2024.12.28 |
| Lesson 10. Prime and composite numbers - Flags #3 (속도 개선-2) (0) | 2024.12.25 |
| Lesson 10. Prime and composite numbers - Flags #2 (속도 개선-1) (0) | 2024.12.25 |
| Lesson 10. Prime and composite numbers - Flags #1 (0) | 2024.12.25 |