반응형
1. 이전 코드 문제점
나누어진 각 블럭에 peak값이 있는지 확인하기 위해, peak 배열을 전체 탐색하고 있다.
예제를 3개의 블럭으로 나눴을 때, 각 블럭에 peak가 있는지, 없는지 어떻게 확인하는지 자세히 뜯어보자.
| A[0] | A[1] | A[2] | A[3] | A[4] | A[5] | A[6] | A[7] | A[8] | A[9] | A[10] | A[11] |
| 1 | 2 | 3 | 4 | 3 | 4 | 1 | 2 | 3 | 4 | 6 | 2 |
index로 나타내면 다음과 같다.
block: (0, 1, 2, 3), (4, 5, 6, 7), (8, 9, 10, 11)
peak: (3, 5, 10)
첫번째 블럭: peak index 3 포함됨
두번째 블럭: peak index 3 미포함 / peak index 5 포함
세번째 블럭: peak index 3 미포함 / peak index 5 미포함 / peak index 10 포함
두번째, 세번째 블럭을 조사할 때,
이미 앞에서 확인된 peak index는 확인할 필요가 없음에도, 확인하고 있다.
2. 속도 개선 아이디어
앞에서 확인된 peak index는 뒤에서 확인하지 않도록 수정한다.
3. 코드 (C++)
코드의 전체적인 흐름은 이전과 동일하다.
peak 구하기 → 약수 구하기 → 약수 정렬 → 최대 블럭 수 구하기
#include <cmath>
#include <algorithm>
int solution(vector<int> &A) {
//peak 구하기
vector<int> peaks = {};
for(size_t i = 1; i < A.size()- 1; i++)
{
if(A[i - 1] < A[i] && A[i] > A[i + 1])
{
peaks.emplace_back(i);
}
}
//peak가 없으면, block도 없다
if(peaks.empty()) return 0;
//약수 구하기
int divisor = 1;
int N = static_cast<int>(A.size());
vector<int> factors = {};
while(divisor < sqrt(N))
{
if(N % divisor == 0)
{
factors.emplace_back(divisor);
factors.emplace_back(N / divisor);
}
divisor++;
}
if(divisor * divisor == A.size()) factors.emplace_back(divisor);
//약수 정렬
sort(factors.begin(), factors.end());
//최대 블럭 수 구하기
//가장 작은 약수 1과, 가장 큰 약수 N은 건너뛴다
for(size_t i = 1; i < factors.size() - 1; i++)
{
int start = 0; //블럭 시작 index
int end = factors[i] - 1; //블럭 끝 index
size_t p = 0;
do
{
//블럭 안에 peak가 있는지 확인
while(p < peaks.size())
{
if(start <= peaks[p] && peaks[p] <= end) break;
p++;
}
if(p >= peaks.size()) break;
start += factors[i];
end += factors[i];
}while(start < N);
if(start >= N) return N / factors[i]; //최대 블럭 수를 찾았다
}
//여기까지 최대 블럭 수를 못찾았다면, 블럭은 1개일수밖에 없다
return 1;
}
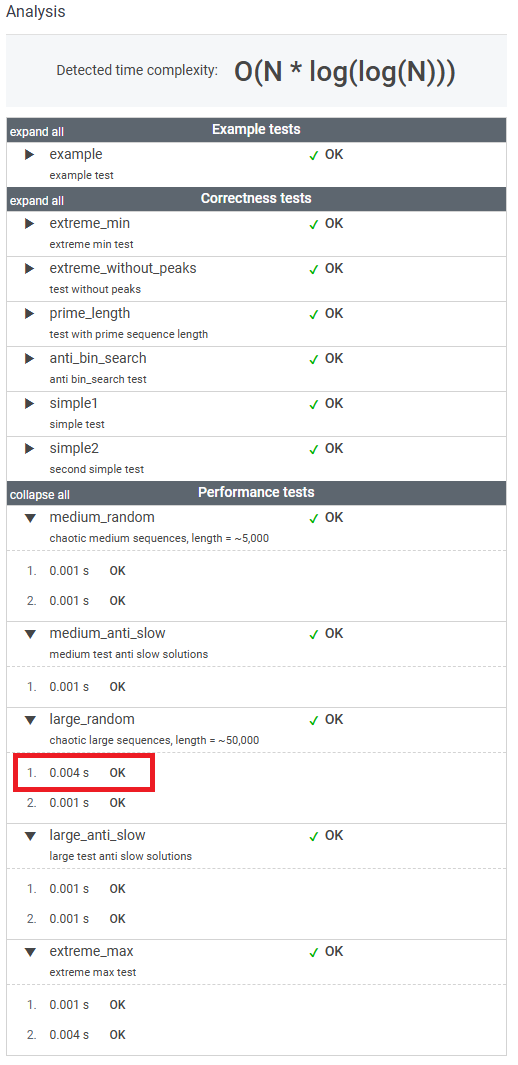
4. 결과
반응형
'Algorithm Problem > Codility' 카테고리의 다른 글
| Lesson 11. Sieve of Eratosthenes - CountNonDivisible #1 (0) | 2024.12.29 |
|---|---|
| Lesson 10. Prime and composite numbers - Peaks #3 (속도 개선-2) (0) | 2024.12.28 |
| Lesson 10. Prime and composite numbers - Peaks #1 (0) | 2024.12.28 |
| Lesson 10. Prime and composite numbers - Flags #4 (번외) (0) | 2024.12.25 |
| Lesson 10. Prime and composite numbers - Flags #3 (속도 개선-2) (0) | 2024.12.25 |