반응형
1. 문제
A non-empty array A consisting of N integers is given.
A peak is an array element which is larger than its neighbours. More precisely, it is an index P such that 0 < P < N − 1 and A[P − 1] < A[P] > A[P + 1].
For example, the following array A:
A[0] = 1
A[1] = 5
A[2] = 3
A[3] = 4
A[4] = 3
A[5] = 4
A[6] = 1
A[7] = 2
A[8] = 3
A[9] = 4
A[10] = 6
A[11] = 2
has exactly four peaks: elements 1, 3, 5 and 10.
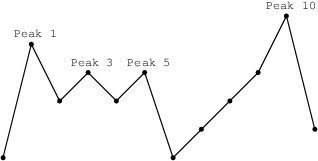
You are going on a trip to a range of mountains whose relative heights are represented by array A, as shown in a figure below. You have to choose how many flags you should take with you. The goal is to set the maximum number of flags on the peaks, according to certain rules.
Flags can only be set on peaks. What's more, if you take K flags, then the distance between any two flags should be greater than or equal to K. The distance between indices P and Q is the absolute value |P − Q|.
For example, given the mountain range represented by array A, above, with N = 12, if you take:
- two flags, you can set them on peaks 1 and 5;
- three flags, you can set them on peaks 1, 5 and 10;
- four flags, you can set only three flags, on peaks 1, 5 and 10.
You can therefore set a maximum of three flags in this case.
Write a function:
int solution(vector<int> &A);
that, given a non-empty array A of N integers, returns the maximum number of flags that can be set on the peaks of the array.
For example, the following array A:
A[0] = 1
A[1] = 5
A[2] = 3
A[3] = 4
A[4] = 3
A[5] = 4
A[6] = 1
A[7] = 2
A[8] = 3
A[9] = 4
A[10] = 6
A[11] = 2
the function should return 3, as explained above.
Write an efficient algorithm for the following assumptions:
- N is an integer within the range [1..400,000];
- each element of array A is an integer within the range [0..1,000,000,000].
Peak에 꽂을 수 있는 Flag 개수를 세는 문제
Peak 조건: \( A[P - 1] < A[P] > A[P + 1], (0 < P < N) \)
Flag 꽂을 수 있는 조건: K개의 Flag를 꽂으려면, 두 깃발 사이의 거리가 K이상이어야 한다
예시) return 3 (1, 5, 10)
| A[0] | A[1] | A[2] | A[3] | A[4] | A[5] | A[6] | A[7] | A[8] | A[9] | A[10] | A[11] |
| 1 | 5 | 3 | 4 | 3 | 4 | 1 | 2 | 3 | 4 | 6 | 2 |
Peak : \( A[1], A[3], A[5], A[10] \)
꽃을 수 있는 Flag 개수 : 3개 \( (A[1] ,A[5], A[10]) \)
2. 매개변수 제한
- Vector A 크기(N): 1 ~ 400,000
- Vector A 값 범위: 0 ~ 1,000,000,000
3. 문제풀이 전략
- Peak 개수를 구한다.
- Peak 간의 거리를 계산한다.
- 만약 Peak 간의 거리가 K이상이면, Flag를 꽂는다.
4. 코드 (C++)
전체 탐색
int solution(vector<int> &A) {
//peak 개수 구하기
vector<int> peaks = {};
for(size_t i = 1; i < A.size() - 1; i++)
{
if(A[i] > A[i - 1] && A[i] > A[i + 1])
{
peaks.emplace_back(i);
}
}
//flag 개수 구하기
int K = static_cast<int>(peaks.size()); // 현재 꽂을 수 있는 최대 flag 수
while(K > 0)
{
int flag_cnt = 1; // 첫번째 peak에는 무조건 flag를 꽂고 시작한다
int distance = 0;
for(int i = 0; i < static_cast<int>(peaks.size()) - 1; i++)
{
distance += peaks[i + 1] - peaks[i]; // 현재 peak와 다음 peak 간의 거리
if(distance >= K) // 두 peak간의 거리가 K 이상이면, flag를 꽂는다
{
distance = 0;
flag_cnt++;
}
}
if(flag_cnt >= K) return K; // K개 만큼 flag를 꽂았다
K--;
}
return 0;
}
5. 결과

반응형
'Algorithm Problem > Codility' 카테고리의 다른 글
| Lesson 10. Prime and composite numbers - Flags #3 (속도 개선-2) (0) | 2024.12.25 |
|---|---|
| Lesson 10. Prime and composite numbers - Flags #2 (속도 개선-1) (0) | 2024.12.25 |
| Lesson 10. Prime and composite numbers - MinPerimeterRectangle (0) | 2024.12.24 |
| Lesson 10. Prime and composite numbers - CountFactors #3 (속도 개선-2) (0) | 2024.12.24 |
| Lesson 10. Prime and composite numbers - CountFactors #2 (속도 개선-1) (1) | 2024.12.24 |