반응형
1. 속도 개선 아이디어
최대 Flag 개수(K)는 Peak 개수와 동일하다.
또한 K만큼 꽂기 위해서는, 최소 \( K * (K - 1) \) 만큼의 거리가 확보되어야 한다.
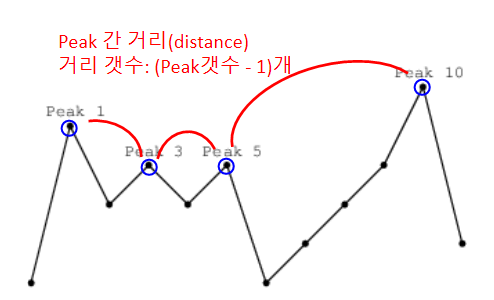
위 성질을 이용하면, 전체 탐색을 줄일 수 있다.
- Peak 개수를 구한다
- Peak 간 '총 거리'를 구한다
- '총 거리'에, (이론적으로) 꽂을 수 있는 최대 Flag 수(K)를 구한다. { 총 거리 \( >= K * (K - 1) \) }
- 구해진 K개를 기준으로, Flag를 꽂을 수 있는지 확인한다.
- 가능하면 return K, 불가능하면 K를 줄여나간다.
2. 코드 (C++)
int solution(vector<int> &A) {
//peak 개수 구하기
vector<int> peaks = {};
for(size_t i = 1; i < A.size() - 1; i++)
{
if(A[i] > A[i - 1] && A[i] > A[i + 1])
{
peaks.emplace_back(i);
}
}
//예외처리
if(peaks.size() == 0) return 0;
else if(peaks.size() == 1) return 1;
//peak 간 총 거리 구하기
int total_distance = 0;
for(int i = 0; i < static_cast<int>(peaks.size()) - 1; i++)
{
int distance = peaks[i + 1] - peaks[i];
total_distance += distance;
}
//peak 간 총 거리에 꽂을 수 있는, 최대 flag 수 구하기
int K = static_cast<int>(peaks.size());
while(K > 0)
{
if( total_distance >= (K * (K - 1)) ) break;
K--;
}
//실제 꽂을 수 있는, flag 수 구하기
while(K > 0)
{
int flag_cnt = 1;
int distance = 0;
for(int i = 0; i < static_cast<int>(peaks.size()) - 1; i++)
{
distance += peaks[i + 1] - peaks[i];
if(distance >= K)
{
distance = 0;
flag_cnt++;
}
}
if(flag_cnt >= K) return K;
K--;
}
return K;
}
3. 결과

반응형
'Algorithm Problem > Codility' 카테고리의 다른 글
| Lesson 10. Prime and composite numbers - Flags #4 (번외) (0) | 2024.12.25 |
|---|---|
| Lesson 10. Prime and composite numbers - Flags #3 (속도 개선-2) (0) | 2024.12.25 |
| Lesson 10. Prime and composite numbers - Flags #1 (0) | 2024.12.25 |
| Lesson 10. Prime and composite numbers - MinPerimeterRectangle (0) | 2024.12.24 |
| Lesson 10. Prime and composite numbers - CountFactors #3 (속도 개선-2) (0) | 2024.12.24 |