1. 속도 개선 아이디어
+1이든, +100이든 흑자만 발생한다면, 가능한 오래 가져가는게 이득이기 때문에, 우리에게 필요한 값은 총 이익값이다.
따라서 이익을 매일 매일 발생하는 이익의 누적으로 바라볼 필요가 있다.
우리가 구하고자 하는 이익이, 매일 발생하는 이익의 누적이라면, 최저값과 최대값의 위치도 신경쓸 필요가 없다.
왜냐하면 중간에 최저값이 있고, 맨 끝에 최대값이 있다고 할 때, 최저값에 사서, 최대값에 파는게 최대 이익인가? 하면 그렇지 않기 때문이다.
최저값 이전에도 계속 흑자가 발생했다면, 그냥 흑자가 발생한 시점부터 쭈욱 가지고 오는게 최대이익이 된다.
Vector A가 아래와 같다고 하자.
| A[0] | A[1] | A[2] | A[3] | A[4] | A[5] | A[6] |
| 5 | 7 | 9 | 6 | 1 | 3 | 4 |
- 매수: A[0] / 매도: A[1] / 이익: A[1] - A[0] = 2
- 매수: A[0] / 매도: A[2] / 이익: A[2] - A[0] = 4
A[2] - A[0]는 (첫째날 이익) + (둘째날 이익)과 같다. \( (A[1] - A[0]) + (A[2] - A[1]) \)
즉, 우리는 매일 발생하는 이익을 더해서, 그 값이 최대 값이 될 때를 구하면, 최대 이익을 알 수 있다..

그렇다면 적자가 발생하면 어떻게 될까?
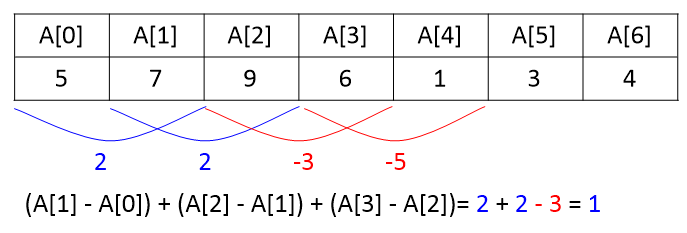
아직 총 이익은 흑자이다.
따라서 앞으로 더 기다리다(확인하다)보면, 총 이익이 더 증가할 수도 있다.
하지만 총 이익이 적자가 된다면?
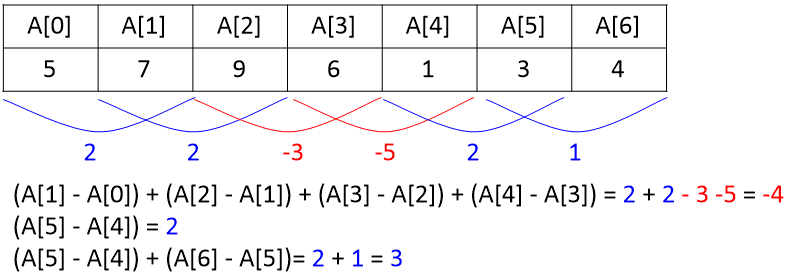
총 이익을 0으로 설정 후, 이익 계산을 다시 시작해야 한다.
2. 예제 분석
return value: 356
| A[0] | A[1] | A[2] | A[3] | A[4] | A[5] |
| 23171 | 21011 | 21123 | 21366 | 21013 | 21367 |
\( A[1] - A[0] = \textcolor{red}{-2160}, \mathsf{누적: 0} \)
\( A[2] - A[1] = \textcolor{blue}{112}, \mathsf{누적: 112} \)
\( A[3] - A[2] = \textcolor{blue}{243}, \mathsf{누적: 355} \)
\( A[4] - A[3] = \textcolor{red}{-353}, \mathsf{누적: 2} \)
\( A[5] - A[4] = \textcolor{blue}{354}, \mathsf{누적: 356} \)
3. 코드 (C++)
int solution(vector<int> &A) {
int max_profit = 0; //최대 이익
int sum_profit = 0; //누적 이익
for(size_t Q = 1; Q < A.size(); Q++)
{
int today_profit = A[Q] - A[Q-1]; //당일 이익
sum_profit += today_profit; //이익 누적하기
if(sum_profit > max_profit) //누적 이익 > 최대 이익
{
max_profit = sum_profit;
}
else if(sum_profit < 0) //누적 이익 초기화
{
sum_profit = 0;
}
}
return max_profit;
}
4. 결과

'Algorithm Problem > Codility' 카테고리의 다른 글
| Lesson 9. Maximum slice problem - MaxDoubleSliceSum #1 (0) | 2024.12.21 |
|---|---|
| Lesson 9. Maximum slice problem - MaxSliceSum (0) | 2024.12.21 |
| Lesson 9. Maximum slice problem - MaxProfit #2 (속도 개선-1) (0) | 2024.12.15 |
| Lesson 9. Maximum slice problem - MaxProfit #1 (0) | 2024.12.15 |
| Lesson 8. Leader - EquiLeader #2 (속도 개선) (0) | 2024.12.13 |