반응형
1. 문제
A non-empty array A consisting of N integers is given.
A triplet (X, Y, Z), such that 0 ≤ X < Y < Z < N, is called a double slice.
The sum of double slice (X, Y, Z) is the total of A[X + 1] + A[X + 2] + ... + A[Y − 1] + A[Y + 1] + A[Y + 2] + ... + A[Z − 1].
For example, array A such that:
A[0] = 3
A[1] = 2
A[2] = 6
A[3] = -1
A[4] = 4
A[5] = 5
A[6] = -1
A[7] = 2
contains the following example double slices:
double slice (0, 3, 6), sum is 2 + 6 + 4 + 5 = 17,
double slice (0, 3, 7), sum is 2 + 6 + 4 + 5 − 1 = 16,
double slice (3, 4, 5), sum is 0.
The goal is to find the maximal sum of any double slice.
Write a function:
int solution(vector<int> &A);
that, given a non-empty array A consisting of N integers, returns the maximal sum of any double slice.
For example, given:
A[0] = 3
A[1] = 2
A[2] = 6
A[3] = -1
A[4] = 4
A[5] = 5
A[6] = -1
A[7] = 2
the function should return 17, because no double slice of array A has a sum of greater than 17.
Write an efficient algorithm for the following assumptions:
- N is an integer within the range [3..100,000];
- each element of array A is an integer within the range [−10,000..10,000].
부분 집합 2개(X, Y, Z)를 더했을 때, 최대 합을 구하는 문제. \( (0 \leq X < Y < Z < N) \)
\( (X, Y, Z) = A[X + 1] + A[X + 2] + ... + A[Y - 1] + A[Y + 1] + A[Y + 2] + A[Z - 1] \)
예시) return 17
| A[0] | A[1] | A[2] | A[3] | A[4] | A[5] | A[6] | A[7] |
| 3 | 2 | 6 | -1 | 4 | 5 | -1 | 2 |
(0, 3, 6) = 2 + 6 + 4 + 5 = 17
(0, 3, 7) = 2 + 6 + 4 + 5 - 1 = 16
(3, 4, 5) = 0
2. 매개변수 제한
- Vector A 크기: 3 ~ 100,000
- Vector A 요소 값: -10,000 ~ 10,000
3. 문제분석
- 맨 처음 요소와 맨 끝 요소는 부분 집합에 포함되지 않는다.
4. 코드 (C++)
전체 탐색 코드
#include <limits>
//부분 집합 합 구하기
int getSum(vector<int>& A, size_t x, size_t y, size_t z)
{
int sum = 0;
for(size_t i = x + 1; i < y; i++)
{
sum += A[i];
}
for(size_t i = y + 1; i < z; i++)
{
sum += A[i];
}
return sum;
}
int solution(vector<int> &A) {
int max = numeric_limits<int>::min();
for(size_t i = 0; i < A.size(); i++)
{
for(size_t j = i + 1; j < A.size(); j++)
{
for(size_t k = j + 1; k < A.size(); k++)
{
int sum = getSum(A, i, j, k);
if(sum > max) max = sum;
}
}
}
return max;
}
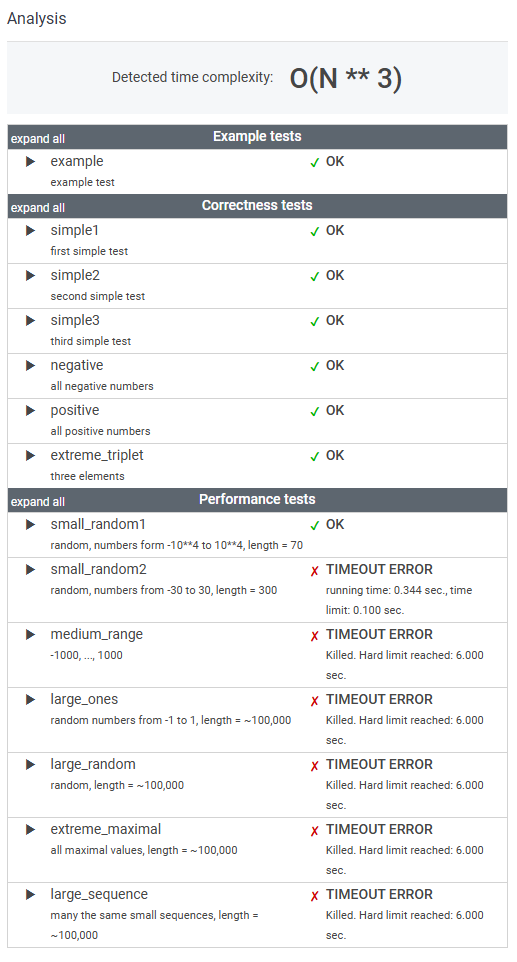
5. 결과
반응형
'Algorithm Problem > Codility' 카테고리의 다른 글
| Lesson 10. Prime and composite numbers - CountFactors #1 (0) | 2024.12.24 |
|---|---|
| Lesson 9. Maximum slice problem - MaxDoubleSliceSum #2 (속도 개선) (1) | 2024.12.21 |
| Lesson 9. Maximum slice problem - MaxSliceSum (0) | 2024.12.21 |
| Lesson 9. Maximum slice problem - MaxProfit #3 (속도 개선-2) (0) | 2024.12.15 |
| Lesson 9. Maximum slice problem - MaxProfit #2 (속도 개선-1) (0) | 2024.12.15 |