1. 속도 개선 아이디어
'Leader는 배열의 절반 이상을 차지해야 한다' 라는 조건에 대한 고찰이 필요하다.
결론부터 얘기하자면, Equi Leader는 배열 전체 Leader와 항상 값이 같다.
전체 배열에 대한 리더(A)가 있다고 하자.
전체 배열을 왼쪽 배열(LEFT)과 오른쪽 배열(RIGHT)로 나누었다.
왼쪽 배열(LEFT)의 리더(B)는 리더(A)와 다른 값이 나올 수 있을까?
오른쪽 배열(RIGHT)의 리더(C)는 리더(A)와 다른 값이 나올 수 있을까?
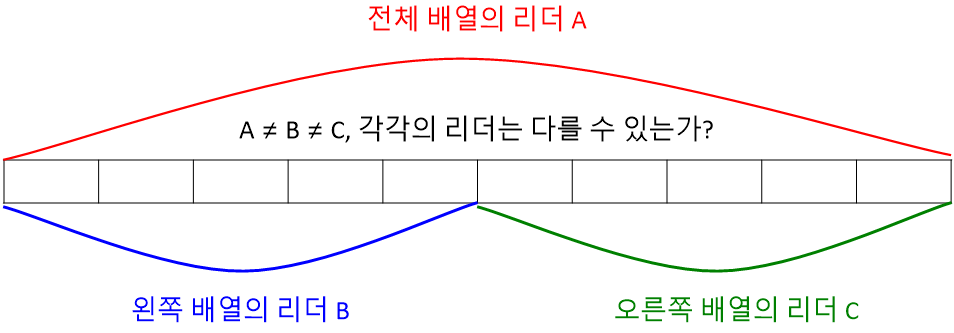
이 질문에 대한 답이, 속도 개선의 열쇠이다.
리더(B)와 리더(C)가 값이 다를 수는 있지만, 둘 중 하나는 반드시 전체 배열 리더(A)와 값이 같다.
즉, Equi Leader가 성립할 때는, 항상 전체 배열 리더(A)와 값이 같다.
증명
결론: 리더(A) \( \neq \) 리더(B) \( \neq \) 리더(C) 가 성립하는 순간, 전체리더(A)는 존재할 수 없다.
전체 배열: N
전체 배열 리더: A
전체 배열 리더 등장 횟수: \( cnt_A \)
A는 리더이므로, \( cnt_A > N \div 2 \) 의 조건을 갖는다.
이제 전체 배열 N에서, 임의의 값 B를 생각해보자.
B의 등장 횟수: \( cnt_B \)
전체 배열 N의 리더는 A이므로, B는 \( cnt_B < N \div 2 \) 의 조건을 갖는다.
따라서 \( cnt_A > cnt_B \) 이고, \( cnt_A + cnt_B \leq N \) 이다.
임의의 값 C가 있다고 하자.
C의 등장 횟수는 \(cnt_C \) 이고, \( cnt_b + cnt_C < N \div 2 \)
아무리 임의의 값이 등장해도, 리더A를 이길 수 없다.
왜냐하면 전체 배열 크기는 고정되어 있기 때문이다.
즉, 리더(A) \( \neq \) 리더(B) \( \neq \) 리더(C) 가 성립하는 순간, 전체리더(A)는 존재할 수 없는 모순이 발생한다.
따라서 리더(B) 혹은 리더(C)는 반드시 리더(A)와 같아야 한다.
다시 말하면, Equi Leader가 성렵하려면, 리더(B)와 리더(C)의 값이, 전체리더(A)와 같아야 한다.
2. 문제풀이 전략
- 전체 리더를 구한다. (전체 리더가 없으면, Equi Leader도 없다)
- 전체 리더 값이 현재 위치(index)에서 몇 번 등장하고 있는지 센다. 단, 좌/우 양쪽에서 각각 세어야 한다
(부분 리더도 전체 리더와 같아야 하므로, 더 이상 리더를 찾을 필요가 없다) - 전체 리더 값이 양쪽의 현재 위치(index)에서 모두 리더가 될 만큼 등장 했다면, Equi Leader가 성립한다.
3. 예제분석
| A[0] | A[1] | A[2] | A[3] | A[4] | A[5] |
| 4 | 3 | 4 | 4 | 4 | 2 |
전체리더: 4
전체리더(4)가 왼쪽(A[0] → A[5])부터 몇 번 등장하는지 부분 합(prefix sums) 알고리즘을 이용해서 구한다.
| A[0] | A[1] | A[2] | A[3] | A[4] | A[5] | ||
| 4 | 3 | 4 | 4 | 4 | 2 | ||
| prefix sum | 0 | 1 | 1 | 2 | 3 | 4 | 4 |
| Left Leader(4) | X | O | X | O | O | O | O |
마찬가지로 전체리더(4)가 오른쪽(A[5] → A[0])부터 몇 번 등장하는지 부분 합(prefix sums) 알고리즘을 이용해서 구한다.
| A[0] | A[1] | A[2] | A[3] | A[4] | A[5] | ||
| 4 | 3 | 4 | 4 | 4 | 2 | ||
| prefix sum | 4 | 3 | 3 | 2 | 1 | 0 | 0 |
| Right Leader(4) | O | O | O | O | X | X | X |
이제 현재 위치(index)에서 prefix sum 값을 보면, 전체리더(4)가 리더로써 등장 했는지 확인할 수 있다.
전체리더(4)가 양쪽(왼쪽/오른쪽) 다 리더인 경우는 2가지 이다.
왼쪽요소 1개 / 오른쪽 요소 5개인 경우 (A[1])
왼쪽요소 3개 / 오른쪽 요소 3개인 경우 (A[3])
4. 코드 (C++)
#include <limits>
int find_leader(vector<int> &A, int start, int end)
{
//cout << "start:" << start << ' ' << "end:" << end << endl;
int leader = 0;
int cnt = 0;
for(int i = start; i < end; i++)
{
if(cnt == 0)
{
leader = A[i];
cnt = 1;
}
else
{
if(A[i] != leader) cnt--;
else cnt++;
}
}
cnt = 0;
for(int i = start; i < end; i++)
{
if(A[i] == leader) cnt++;
}
if( cnt <= ((end - start) / 2) )
{
return numeric_limits<int>::min();
}
return leader;
}
int solution(vector<int> &A) {
//find the leader in vector A
int leader = find_leader(A, 0, A.size());
if(leader == numeric_limits<int>::min()) return 0;
//prefix sum of left side
vector<int> left_leader_cnt(A.size() + 1, 0);
for(size_t i = 0; i < A.size(); i++)
{
left_leader_cnt[i + 1] = left_leader_cnt[i];
if(A[i] == leader) left_leader_cnt[i + 1] += 1;
}
//prefix sum of right side
vector<int> right_leader_cnt(A.size() + 1, 0);
for(int i = static_cast<int>(A.size() - 1); i >= 0; i--)
{
right_leader_cnt[i] = right_leader_cnt[i + 1];
if(A[i] == leader) right_leader_cnt[i] += 1;
}
//find equiLeader
int cnt = 0;
for(int i = 0; i < static_cast<int>(left_leader_cnt.size()); i++)
{
if( left_leader_cnt[i] <= (i / 2) ) continue;
if( right_leader_cnt[i] <= static_cast<int>(A.size() - i) / 2 ) continue;
cnt++;
}
return cnt;
}
5. 결과
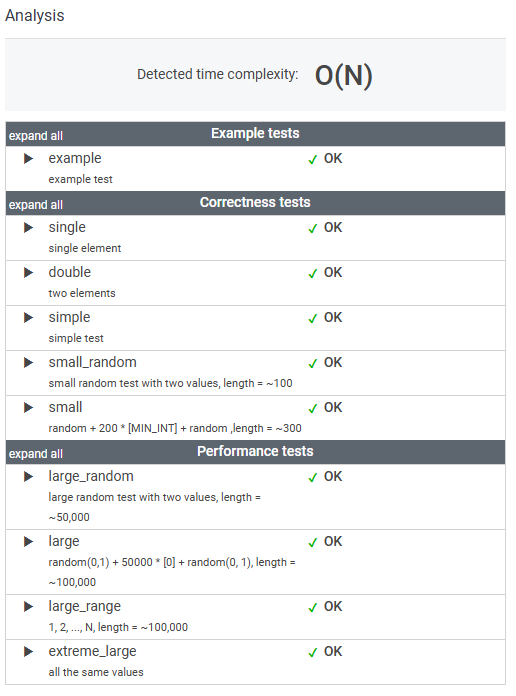
'Algorithm Problem > Codility' 카테고리의 다른 글
| Lesson 9. Maximum slice problem - MaxProfit #2 (속도 개선-1) (0) | 2024.12.15 |
|---|---|
| Lesson 9. Maximum slice problem - MaxProfit #1 (0) | 2024.12.15 |
| Lesson 8. Leader - EquiLeader #1 (0) | 2024.12.13 |
| Lesson 8. Leader - Dominator #3-2 (코드 개선) (1) | 2024.12.13 |
| Lesson 8. Leader - Dominator #3-1 (0) | 2024.12.13 |