반응형
1. 문제
The Fibonacci sequence is defined using the following recursive formula:
F(0) = 0
F(1) = 1
F(M) = F(M - 1) + F(M - 2) if M >= 2
A small frog wants to get to the other side of a river. The frog is initially located at one bank of the river (position −1) and wants to get to the other bank (position N). The frog can jump over any distance F(K), where F(K) is the K-th Fibonacci number. Luckily, there are many leaves on the river, and the frog can jump between the leaves, but only in the direction of the bank at position N.
The leaves on the river are represented in an array A consisting of N integers. Consecutive elements of array A represent consecutive positions from 0 to N − 1 on the river. Array A contains only 0s and/or 1s:
- 0 represents a position without a leaf;
- 1 represents a position containing a leaf.
The goal is to count the minimum number of jumps in which the frog can get to the other side of the river (from position −1 to position N). The frog can jump between positions −1 and N (the banks of the river) and every position containing a leaf.
For example, consider array A such that:
A[0] = 0
A[1] = 0
A[2] = 0
A[3] = 1
A[4] = 1
A[5] = 0
A[6] = 1
A[7] = 0
A[8] = 0
A[9] = 0
A[10] = 0
The frog can make three jumps of length F(5) = 5, F(3) = 2 and F(5) = 5.
Write a function:
- int solution(vector<int> &A);
that, given an array A consisting of N integers, returns the minimum number of jumps by which the frog can get to the other side of the river. If the frog cannot reach the other side of the river, the function should return −1.
For example, given:
A[0] = 0
A[1] = 0
A[2] = 0
A[3] = 1
A[4] = 1
A[5] = 0
A[6] = 1
A[7] = 0
A[8] = 0
A[9] = 0
A[10] = 0
the function should return 3, as explained above.
Write an efficient algorithm for the following assumptions:
- N is an integer within the range [0..100,000];
- each element of array A is an integer that can have one of the following values: 0, 1.
강을 건너기 위한 최소 점프 수를 구하는 문제.
조건
- 강을 건너는 방향은 (0 → N) 이다.
- 강 위에 있는 잎(leaf)으로 점프 할 수 있다.
단, 점프는 피보나치 수로만 할 수 있다. - 점프가 가능한 범위는 N까지이다.
N을 넘어가는 점프는 불가능하다. (N을 초과하는 피보나치 수로 한방에 점프하는 것은 안된다)
예제) return 3
A[i] = 0; 잎이 없다.
A[i] = 1; 잎이 있다.
| A[0] | A[1] | A[2] | A[3] | A[4] | A[5] | A[6] | A[7] | A[8] | A[9] | A[10] | Arrival |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
A[3] = 점프 불가 (피보나치 수 아님)
A[4] = 점프 가능 (피보나치 수 , F(5) = 5)
A[6] = 점프 가능 (피보나치 수 , F(3) = 2)
Arrival = 점프 가능 (피보나치 수 , F(5) = 5)
2. 매개변수 조건
Vector A 크기: 0 ~ 100,000
Vector A 값 범위 : 0 or 1
3. 예제 분석
Vector A가 0부터 시작해서, 피보나치 수와 안맞는다.
따라서 다음과 같이 생각해야 한다.
| A[0] | A[1] | A[2] | A[3] | A[4] | A[5] | A[6] | A[7] | A[8] | A[9] | A[10] | A[11] | A[12] |
| Start | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | Arrival |
A[0] 과 A[12]의 값은 1이다.
4. 문제풀이 전략
- F(K) <= A.size() + 1 을 만족하는 피보나치 수를 미리 계산해둔다.
- 점프 가능한 위치들만 별도 Vector로 만든다. (leaves)
- 현재 위치에서 점프 가능한 다음 위치를 찾는다.
5. 코드 (C++)
재귀 함수로 구현
//Count the minimum number of jumps to the other side of a river
void Calculate(int cur_pos, int cur_jump, int& min_jump, vector<int>& fib, vector<int>& leaves)
{
//arrived at the destination
if(leaves[cur_pos] == leaves.back())
{
if(cur_jump < min_jump) min_jump = cur_jump;
return;
}
//find a leaf to jump on
for(size_t i = cur_pos + 1; i < leaves.size(); i++)
{
//The leaf to jump on should be at a distance of a Fibonacci number
auto it = find(fib.begin() + 2, fib.end(), leaves[i] - leaves[cur_pos]);
if(it == fib.end()) continue;
Calculate(i, cur_jump + 1, min_jump, fib, leaves);
}
}
int solution(vector<int> &A) {
int destination = A.size() + 1;
//generate fibonacci numbers
vector<int> fib = {};
fib.emplace_back(0);
fib.emplace_back(1);
int M = 2;
int n = fib[1] + fib[0];
while(n <= destination)
{
fib.emplace_back(n);
M++;
n = fib[M - 1] + fib[M - 2];
}
//generate leaves vector that contains only the leaves that can be jumped to
vector<int> leaves = {};
leaves.emplace_back(0);
for(size_t i = 0; i < A.size(); i++)
{
if(A[i] == 1) leaves.emplace_back(i + 1);
}
leaves.emplace_back(destination);
//Count the minimum number of jumps to the other side of a river
int min_jump = numeric_limits<int>::max();
for(size_t i = 1; i < leaves.size(); i++)
{
auto it = find(fib.begin() + 2, fib.end(), leaves[i]);
if(it == fib.end()) continue;
Calculate(i, 1, min_jump, fib, leaves);
}
if(min_jump == numeric_limits<int>::max()) return -1;
return min_jump;
}
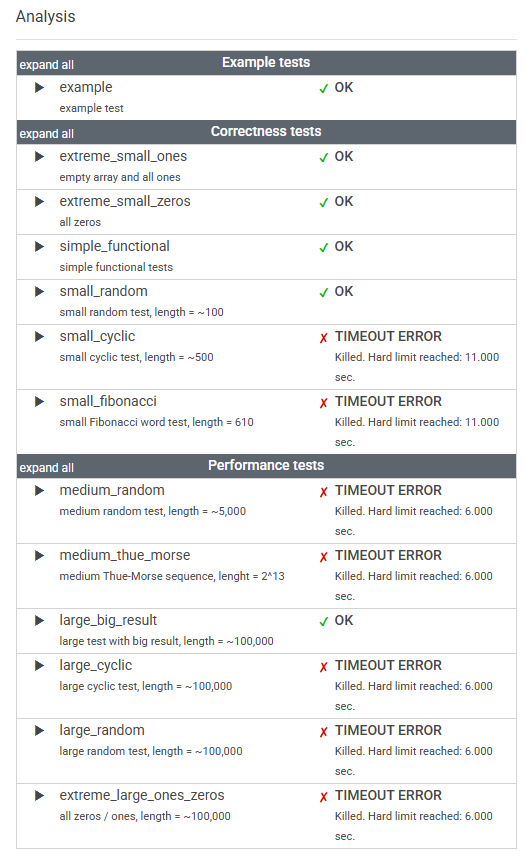
6. 결과
반응형
'Algorithm Problem > Codility' 카테고리의 다른 글
| Lesson 13. Fibonacci numbers - FibFrog #3 (속도 개선) (0) | 2025.01.27 |
|---|---|
| Lesson 13. Fibonacci numbers - FibFrog #2 (속도 개선) (0) | 2025.01.27 |
| Lesson 12. Euclidean algorithm - CommonPrimeDivisors #4 (개선-3) (0) | 2025.01.18 |
| Lesson 12. Euclidean algorithm - CommonPrimeDivisors #3 (개선-2) (0) | 2025.01.18 |
| Lesson 12. Euclidean algorithm - CommonPrimeDivisors #2 (개선-1) (0) | 2025.01.18 |