반응형
1. 속도 개선 아이디어
두 수(N, M)의 밑이 같다면, 두 수의 소인수는 최대공약수의 밑으로만 구성이 되어있다.
(10, 30)의 최대공약수(GCD)를 구해보자.
\( 10 = 2 \times 5 \)
\( 30 = 2 \times 3 \times 5 \)
\( GCD = 2 \times 5 \)
최대공약수를 이용해서 두 수의 소인수를 제거 했을 때, 제거되지 않는 소인수가 있다면?
이건 그 수만 가지고 있는 소인수가 된다.
즉, 두 수의 소인수는 같지 않다라는 결론에 도달할 수 있다.
이 방법은 소인수의 밑을 찾을 때, 최대공약수를 활용하므로, 이전 코드에서의 불필요한 연산을 줄일 수 있다.
이전코드에서는 10과 1000이 같은 소인수들을 가지고 있는지 확인하려면, 10과 1000의 모든 소인수들을 구하고 비교했다.
하지만 최대공약수를 활용한다면, 최대공약수(10)의 소인수만을 구하고, 10과 30을 최대공약수의 소인수의 밑으로 나눠보면 된다. 최대공약수의 밑으로 나눴을 때, 1이 된다면, 그 수는 최대공약수의 밑으로만 구성된 수가 된다.
2. 문제풀이 전략
- 최대공약수를 구한다
- 최대공약수의 소인수를 구한다
- 최대공약수의 소인수로 A[i]와 B[i]를 나눈다 (= A와 B에서 최대공약수의 소인수를 제거한다)
- A와 B에 남아 있는 소인수를 최대공약수의 밑으로 나눈다
- A, B가 최종적으로 1이 된다면, 소인수의 밑이 같은 것이다
- 만약 2이상이 된다면, 최대공약수와 다른 소인수의 밑을 갖고 있는 것이다
3. 코드 (C++)
#include <cmath>
#include <map>
//최대공약수 구하기
int GetCGD(int a, int b)
{
if(a % b == 0) return b;
else return GetCGD(b, a % b);
}
//소인수 구하기
map<int, int> GetPrimeDivisors(int n)
{
map<int, int> prime_divisors = {}; //map<base, exponent>
int i = 2;
while(i <= n)
{
if(n % i == 0) // i는 소인수
{
auto it = prime_divisors.find(i);
if(it == prime_divisors.end())
{
prime_divisors.insert(pair<int, int>(i, 1));
}
else
{
it->second += 1;
}
// n을 i로 나누어서, n 값을 줄인다
// 소인수 i가 여러번 쓰일수도 있기 때문에, i값을 증가시키면 안된다.
n /= i;
}
else //i는 n의 소인수가 아니다
{
i++;
}
}
return prime_divisors;
}
//최대공약수와 소인수가 같은지 확인
bool CommonPrimeDivisors(int n, map<int, int>& gcd_divisors)
{
auto it = gcd_divisors.begin();
while(it != gcd_divisors.end() && n > 1)
{
if(it->first > n) break;
if(n % it->first == 0) n /= it->first;
else it++;
}
if(n > 1) return false;
return true;
}
int solution(vector<int> &A, vector<int> &B) {
int cnt = 0;
for(size_t i = 0; i < A.size(); i++)
{
//예외처리
if(A[i] == B[i])
{
cnt++;
continue;
}
int gcd = GetCGD(A[i], B[i]);
if(gcd <= 1) continue; // 최대공약수가 1이면, 서로소
//최대공약수(GCD)의 소인수 구하기
map<int, int> gcd_divisors = GetPrimeDivisors(gcd);
//A[i], B[i]소인수가 최대공약수(GCD) 소인수와 같은지 확인
int a = A[i] / gcd; //최대공약수의 소인수는 제거하고 시작한다
bool same = CommonPrimeDivisors(a, gcd_divisors);
if(!same) continue;
int b = B[i] / gcd; //최대공약수의 소인수는 제거하고 시작한다
same = CommonPrimeDivisors(b, gcd_divisors);
if(!same) continue;
cnt++;
}
return cnt;
}
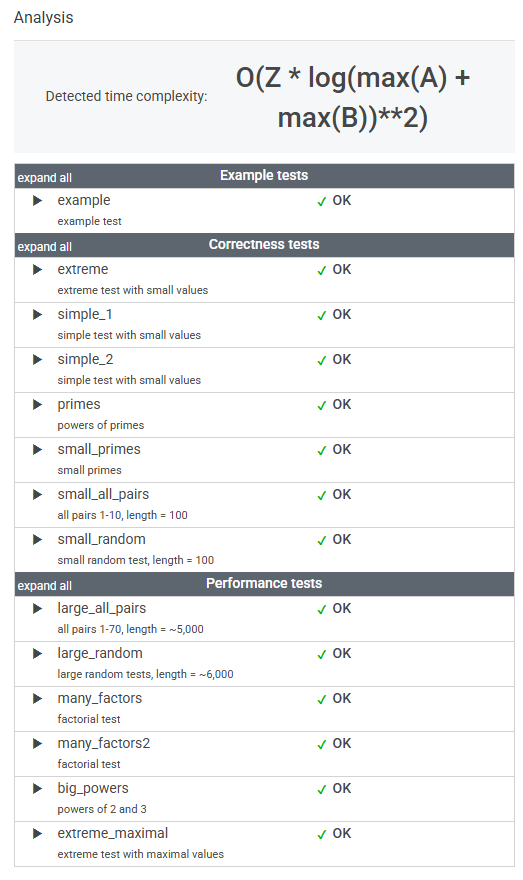
4. 결과
반응형
'Algorithm Problem > Codility' 카테고리의 다른 글
| Lesson 13. Fibonacci numbers - FibFrog #2 (속도 개선) (0) | 2025.01.27 |
|---|---|
| Lesson 13. Fibonacci numbers - FibFrog #1 (0) | 2025.01.27 |
| Lesson 12. Euclidean algorithm - CommonPrimeDivisors #3 (개선-2) (0) | 2025.01.18 |
| Lesson 12. Euclidean algorithm - CommonPrimeDivisors #2 (개선-1) (0) | 2025.01.18 |
| Lesson 12. Euclidean algorithm - CommonPrimeDivisors #1 (0) | 2025.01.18 |