반응형
1. 문제
Two positive integers N and M are given. Integer N represents the number of chocolates arranged in a circle, numbered from 0 to N − 1.
You start to eat the chocolates. After eating a chocolate you leave only a wrapper.
You begin with eating chocolate number 0. Then you omit the next M − 1 chocolates or wrappers on the circle, and eat the following one.
More precisely, if you ate chocolate number X, then you will next eat the chocolate with number (X + M) modulo N (remainder of division).
You stop eating when you encounter an empty wrapper.
For example, given integers N = 10 and M = 4. You will eat the following chocolates: 0, 4, 8, 2, 6.
The goal is to count the number of chocolates that you will eat, following the above rules.
Write a function:
int solution(int N, int M);
that, given two positive integers N and M, returns the number of chocolates that you will eat.
For example, given integers N = 10 and M = 4. the function should return 5, as explained above.
Write an efficient algorithm for the following assumptions:
- N and M are integers within the range [1..1,000,000,000].
원형 케이크에서 먹을 수 있는 케이크 조각의 수를 세는 문제
규칙
- 케이크 조각에는 0부터 (N - 1)까지 번호가 붙어있다.
- X번째 조각을 먹으면, 다음에는 (X + M)번째 조각을 먹어야 한다.
- 먹어야할 조각이 이미 먹은 조각이면, 그만 먹는다.
예시
- N = 10, M = 4
- 케이크 조각 먹게 되는 순서: 0, 4, 8, 2, 6
- 먹은 케이크 조각 수: 5
2. 매개변수 조건
- N: 1 ~ 1,000,000,000
- M: 1 ~ 1,000,000,000
3. 문제 분석
- 케이크 조각 번호의 순서:
첫 번째 조각(0번)을 먹고 나면,
두 번째 조각은 (0 + M) % N번,
세 번째 조각은 (M + M) % N번, ... 이 된다. - 원형 배열에서의 반복:
이 과정에서 중요한 점은, 케이크가 원형이기 때문에 결국 이미 먹었던 조각으로 돌아오게 된다는 것이다.
그리고 돌아오는 것은, M의 배수들이 원형으로 돌아오는 주기와 연관이 있다. 이 주기가 정확히 얼마나 걸리는지를 결정하는 것은 (N, M)의 최대공약수이다. - 최대공약수의 역할:
만약 (N, M)의 최대공약수가 1이라면, 모든 조각을 다 먹게 된다.
그러나 (N, M)의 최대공약수가 2 이상이라면, 우리가 방문하는 조각의 번호는 일정한 간격으로 반복된다.
예를 들어, (N, M)의 최대공약수가 2일 경우, 먹게되는 조각의 수는 N / 2 된다.
4. 코드 (C++)
최대공약수 알고리즘 관련 글을 여기로
int solution(int N, int M) {
int gcd = 0;
if(N % M == 0) gcd = M;
int a = N;
int b = M;
while(b != 0)
{
int temp = a % b;
if(temp == 0)
{
gcd = b;
break;
}
a = b;
b = temp;
}
return N / gcd;
}
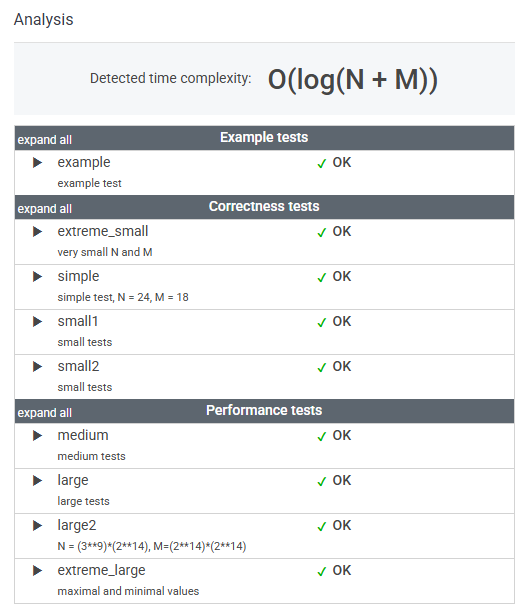
5. 결과
반응형
'Algorithm Problem > Codility' 카테고리의 다른 글
| Lesson 12. Euclidean algorithm - CommonPrimeDivisors #2 (개선-1) (0) | 2025.01.18 |
|---|---|
| Lesson 12. Euclidean algorithm - CommonPrimeDivisors #1 (0) | 2025.01.18 |
| Lesson 11. Sieve of Eratosthenes - CountSemiPrimes #3 (속도 개선-2) (0) | 2025.01.03 |
| Lesson 11. Sieve of Eratosthenes - CountSemiPrimes #2 (속도 개선-1) (0) | 2025.01.02 |
| Lesson 11. Sieve of Eratosthenes - CountSemiPrimes #1 (0) | 2025.01.01 |