1. 문제
We draw N discs on a plane. The discs are numbered from 0 to N − 1. An array A of N non-negative integers, specifying the radiuses of the discs, is given. The J-th disc is drawn with its center at (J, 0) and radius A[J].
We say that the J-th disc and K-th disc intersect if J ≠ K and the J-th and K-th discs have at least one common point (assuming that the discs contain their borders).
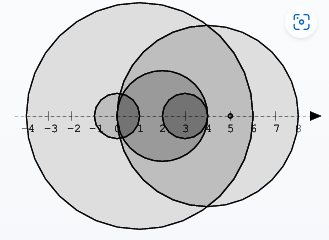
The figure below shows discs drawn for N = 6 and A as follows:
A[0] = 1
A[1] = 5
A[2] = 2
A[3] = 1
A[4] = 4
A[5] = 0
There are eleven (unordered) pairs of discs that intersect, namely:
- discs 1 and 4 intersect, and both intersect with all the other discs;
- disc 2 also intersects with discs 0 and 3.
Write a function:
int solution(vector<int> &A);
that, given an array A describing N discs as explained above, returns the number of (unordered) pairs of intersecting discs. The function should return −1 if the number of intersecting pairs exceeds 10,000,000.
Given array A shown above, the function should return 11, as explained above.
Write an efficient algorithm for the following assumptions:
- N is an integer within the range [0..100,000];
- each element of array A is an integer within the range [0..2,147,483,647].
주어진 배열을 이용해서 원을 그렸을 때, 교차 혹은 포함하는 원의 갯수를 구하는 문제.
원을 그리는 방법은 다음과 같다.
원의 중심: index
반지름: value
즉, A[i]는 i를 중심으로 A[i]를 반지름으로 하는 원을 그린다.
2. 매개변수 제한
Vector A 크기: 0 ~ 100,000
Vector A 요소 값 범위: 0 ~ 2,147,483,647
3. 문제 분석
결론: 빨간색(오른쪽) >= 파란색(왼쪽)이면 교차 혹은 포함이다.
이유:
원이 교차하는 경우는 세 가지이다.
(아래 그림은 빨간원을 기준으로 다른 원과 교차하는지 확인한다.)
 |
 |
 |
| 일부 겹치는 경우1 | 일부 겹치는 경우2 | 포함하는 경우 |
그럼 교차하는 조건을 뽑아보자.
| 일부 겹치는 경우1 | 일부 겹치는 경우2 | 포함하는 경우 |
| 빨간색(왼쪽) > 파란색(왼쪽) | 빨간색(왼쪽) < 파란색(왼쪽) | 빨간색(왼쪽) < 파란색(왼쪽) |
| 빨간색(왼쪽) < 파란색(오른쪽) | 빨간색(왼쪽) < 파란색(오른쪽) | 빨간색(왼쪽) < 파란색(오른쪽) |
| 빨간색(오른쪽) > 파란색(왼쪽) | 빨간색(오른쪽) > 파란색(왼쪽) | 빨간색(오른쪽) > 파란색(왼쪽) |
| 빨간색(오른쪽) > 파란색(오른쪽) |
빨간색(오른쪽) < 파란색(오른쪽) | 빨간색(오른쪽) > 파란색(오른쪽) |
모든 경우(일부 겹치는 경우 1, 2 및 포함)에 공통적으로 뽑히는 조건은 두 가지 이다.
하지만 빨간색(왼쪽) < 파란색(오른쪽) 조건은 두 원이 교차하지 않을 때도 성립하는 조건이다.
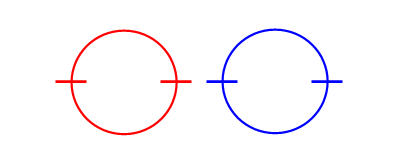
즉, 두 원이 교차하는 조건은 빨간색(오른쪽)이 파란색(왼쪽) 보다 큰 경우이다 = 빨간색(오른쪽) > 파란색(왼쪽)
물론 빨간색(오른쪽) > 파란색(왼쪽)도 교차하지 않는 조건이 있지만 이 조건은 고려할 필요가 없다.
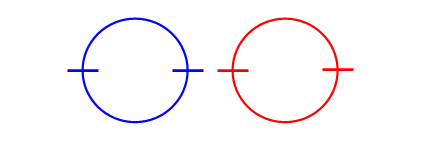
왜냐하면, 이 문제는 0번째부터 index 값이 증가하면서 순차적으로 원을 그리고 있기 때문이다.따라서 우리도 내 왼쪽에 무엇이 있는지 신경쓰지 말고, 내 오른쪽에 있는 원들을 순차적으로 비교해가면 된다.

4. 예제 분석
| 원점(index) | 반지름(value) | 왼쪽 값 | 오른쪽 값 |
| 0 | 1 | -1 | 1 |
| 1 | 5 | -4 | 6 |
| 2 | 2 | 0 | 4 |
| 3 | 1 | 2 | 4 |
| 4 | 4 | 0 | 8 |
| 5 | 0 | 5 | 5 |
A[0]의 오른쪽 값보다 작거나 같은 왼쪽 값을 가지는 원 : A[1], A[2], A[4]
A[1]의 오른쪽 값보다 작거나 같은 왼쪽 값을 가지는 원 : A[2], A[3], A[4], A[5]
A[2]의 오른쪽 값보다 작거나 같은 왼쪽 값을 가지는 원 : A[3], A[4]
A[3]의 오른쪽 값보다 작거나 같은 왼쪽 값을 가지는 원 : A[4]
A[4]의 오른쪽 값보다 작거나 같은 왼쪽 값을 가지는 원 : A[5]
A[5]의 오른쪽 값보다 작거나 같은 왼쪽 값을 가지는 원 : 없음(끝)
5. 코드 (C++)
#include <cstdint>
int solution(vector<int> &A) {
int cnt = 0;
for(size_t i = 0; i < A.size(); i++)
{
int64_t right_value = i + A[i];
for(size_t j = i + 1; j < A.size(); j++)
{
int64_t left_value = j - A[j];
if(left_value <= right_value) cnt++;
if(cnt > 10000000) return -1;
}
}
return cnt;
}
6. 결과

'Algorithm Problem > Codility' 카테고리의 다른 글
| Lesson 7. Stacks and Queues - Brackets (1) | 2024.11.24 |
|---|---|
| Lesson 6. Sorting - NumberOfDiscIntersections #2 (속도 개선) (0) | 2024.11.23 |
| Lesson 6. Sorting - Triangle #2 (속도개선) (1) | 2024.11.15 |
| Lesson 6. Sorting - Triangle #1 (0) | 2024.11.14 |
| Lesson 6. Sorting - MaxProductOfThree (0) | 2024.11.10 |